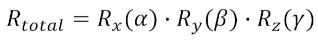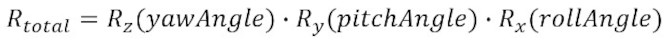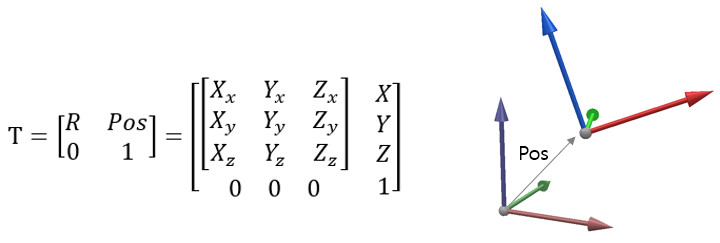On positions, orientations & transformations

In CoppeliaSim there are many different ways to get, set, or work with positions & orientations. Following nomenclature is used throughout this user manual:

Euler angles

The Euler angles are three angles that describe a rotation, the orientation of a rigid body, or the orientation of a frame. There are twelve different conventions when talking about Euler angles. They can be grouped into Proper Euler angles, and Tait-Bryan angles where the latter represents rotations about three distinct axes. In CoppeliaSim, Tait-Bryan angles alpha, beta and gamma (or (a,b,g)) are used, describing a rotation composed by three elemental rotations:

[Euler angles convention in CoppeliaSim]

where Rz, Ry and Rx represent elemental rotations about axes Z, Y and X respectively (in that order), of the absolute reference frame.

For a rigid body, or scene object, you can obtain the same transformation if you rotate it in following order about its own reference frame: rotation of alpha about own x, followed by a rotation of beta about own y, followed by a rotation of gamma about own z.

Yaw-Pitch-Roll are also Tait-Bryan angles describing a rotation composed by three elemental rotations:

[Yaw-Pitch-Roll rotations]

where Rx, Ry and Rz represent elemental rotations about axes X, Y and Z respectively (in that order), of the absolute reference frame.

Use following API functions to convert between alpha-beta-gamma angles and yaw-pitch-roll angles:

Quaternions

Quaternions are four values that uniquely describe a rotation, the orientation of a rigid body, or the orientation of a frame. They are superior to Euler angles in several ways (e.g. no gimbal lock), but are more difficult to understand and construct. For that reason they are never used in user interfaces, but preferred when working with orientations in code. In CoppeliaSim, quaternions are expressed as a 4-element table: (Qx,Qy,Qz,Qw), where (Qx,Qy,Qz) is the rotation axis unit vector multiplied by sin(angle/2), and Qw is cos(angle/2), where angle is the rotation angle. Following API functions can be used to convert between quaternions, Euler angles and matrices:

Rotation matrices

A rotation matrix is a 3x3 matrix that describes a rotation, the orientation of a rigid body, or the orientation of a frame:

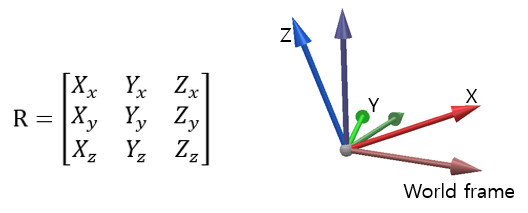
[Rotation matrix in 3D space]

In above matrix, unit vectors (Xx,Xy,Xz), (Yx,Yy,Yz) and (Zx,Zy,Zz) represent the reference frame's axis X, Y and Z respectively. In CoppeliaSim, rotation matrices are expressed as a 9-element table in row-major order: (Xx,Yx,Zx,Xy,Yy,Zy,Xz,Yz,Zz). See also following API functions related to rotation matrices:

Transformation matrices

A transformation matrix is a 4x4 matrix that describes a frame-frame transformation in 3D space. The first 3x3 elements of the matrix represent a rotation matrix:

[Transformation matrix in 3D space]

In CoppeliaSim, transformation matrices are expressed as a 12-element table in row-major order (the last row is omitted): (Xx,Yx,Zx,X,Xy,Yy,Zy,Y,Xz,Yz,Zz,Z). See also following API functions related to rotation matrices:

Poses

Poses are values that describe a frame transformation in 3D space. In CoppeliaSim, poses are expressed as a 7-element table: (X,Y,Z,Qx,Qy,Qz,Qw), i.e. a position followed by a quaternion. See also following API functions related to poses: